The freehand modeling of three-dimensional human faces with an usual 3D-animation software is still a big challenge for many CG Artists. A problem during the modeling process of real, human-like characters is the observance of certain natural proportions. An important role plays the famous Golden Ratio, which is difficult to be applied in many ways.
In this paper I will describe some application possibilities of the Golden Ratio during the 3D modeling process, regardless of the used 3d software.Necessary for the application of this workaround is a semi-complete mesh scan or something else to which the templates of the Golden Ratio can be applied. The pattern we construct in 3D is the Phi Mask (or Golden Mask) of Dr. Stephen R. Marquardt of the Loma Linda University and the University of Southern California (1). He claims it represents the ideal facial archetype. Many designers and cosmetic surgeons have found his mask convincing. But the mask is not an ideal pattern for all character types, including non-European and sub-Saharan or East Asians. The female pattern of the Phi Mask is an approximation of a masculinized Caucasian female picture, given by the general public that strongly and overwhelmingly prefers above average facial femininity in women (2). This pattern should also not be applied to extravagant or comic styled characters. The ideal of human beauty is not absolute, but comes out of the relationship of individual parts.
Download
Download this paper as PDF: The Golden Ratio in 3D Face Modelling
Download the MAX (2010) File: PhiMask
1. Introduction
The Golden Ratio is an irrational mathematic constant which has fascinated mathematicians in ancient Greece at least 2,500 years ago. The number is the result of the following equation:
![]()
The ratio divides a line into two parts with (a) 61,8% and 38,2 %. This means that the bigger acts to smaller one as the sum of the two to the larger ones. This property is an example of self-similarity. By subtracting the shorter of the two distances from the longer the result is an even shorter distance a-b with the distance to the turn in the ratio b of the Golden Ratio Φ. Not only mathematicians but also artists discovered the golden ratio as an important tool for harmonious and aesthetic divisions in pictures, statues and buildings. »De Divina Proportione« (About the divine proportions) from Luca Pacioli and illustrated by Leonardo da Vinci is a very famous book about mathematical and artistic proportions. It shows one of the first drawings of a human face in relation to the Golden Ratio. (3)
Figure 1: Illustration from Luca Pacioli’s De Divina Proportione applies geometric proportions to the human face. (Wikipedia)
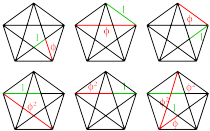
The geometrical figures with the closest relationship to the Golden Ratio and the human face are the pentagon and pentagram. Each intersection of edges sections other edges in the golden ratio. Also, the ratio of the length of the shorter segment to the segment bounded by the 2 intersecting edges (a side of the pentagon in the pentagram’s center) is Φ. The pentagram includes ten isosceles triangles: five acute and five obtuse isosceles triangles. In all of them, the ratio of the longer side to the shorter side is φ. (1)
Figure 2: Pentagon and pentagram in relationship to the Golden Ratio
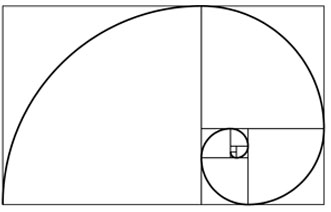
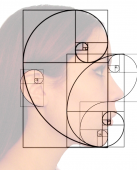
Another shape of the human face with a close connection to the Golden Ratio is the Fibbonaci Spiral. Johannes Kepler found out, that the quotient of two successive Fibonacci numbers approaches to the Golden Ratio Φ.
![]()
Figure 3: A Fibonacci spiral which approximates the golden spiral, using Fibonacci sequence square sizes up to 34 (Wikipedia)
But what is the connection of the pentagon, the pentagram, the Fibbonaci Spiral with the human face? These geometric shapes may be useful during the 3d modeling process (they are really simple to create with 3d software application), but in what respect the Golden Ratio is the human face of modeling? To use the Golden Ratio for the human face modeling process we need some more information about the real one.
2. Research
The FaceResearch Lab of the University of Aberdeen in Scotland developed an interactive online web application to merge different human faces of different people to one average image. To make a statement about the Golden Ratio of the common average human face we combine so many faces as possible. Of course this statement can also be applied to real or individual faces, but this could be seen as a coincidence in particularly harmonious or attractive faces. By taking a closer look to a composed image created by this software we see Golden Ratios all over the face (Figure 4).
Figure 4: An average human face and the Golden Ratio (Image: FaceResearch Lab, http://www.faceresearch.org/demos/average)
The Golden Ratio describes only the relationship of two distances and their length. The Fibonacci spiral extends this into a curve or a spiral. It is very clear when we look at the profile of a human face from the side and apply this shape on it. We see Fibonacci spirals with different scales and get sequences of the Fibonacci curve with different square sizes.
Figure 5: Fibonacci spirals in the human face from the side
3. 2D Face Masks
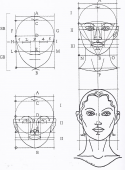
The versatile shape of the head has been subject of many studies since the ancient Greece. Many artists and scientists have contributed their observations to determine the rules of proportion in the face. Leonardo da Vinci discovered that the perfect oval must be divided into three equal sections. These sections (Figure 6) goes from the hairline at the top to the highest point of the eyebrow (I) to the nose (II) and finally to the bottom tip of the chin. (III) (3)
Figure 6: Leonardo da Vincis three divisions of the female face (3).
Another interesting method is from Ingeborg Bernard: To determine the volume of the skull, you can draw a rectangle with an aspect ratio of 2:3. Then you divide the length into three equal sections and suggest a circle with a radius of one third of the length. The diameter corresponds to the largest width of the skull. The basic volume of the smaller skull face is obtained by a circle whose center axis is between the eyes and chin. The basic shape of the face is formed by tangential connections between the two circles. The head is as wide as five eyes. The eye axis is located at half the height of the head and the distance between the eyes is one eye width. The face can is divided into the three sections of da Vinci: from top to brow, then nose to the base and from there to the chin. The distance from the mouth to the corner of your eye is as big as the ear is high. The nasal base is as wide as an eye. (4)
Figure 7: Reproductions of works by Ingeborg Bernhard and uploaded by Wikipedia. Released under the GFDL and CC-BY-SA-all licences. (4)
Disadvantage of all drawings and front proportions is that we have no information about the gradient of the right proportion values in depth. To create a 3D mask we need an extended mask system with this additional information about the right proportions of the human face.
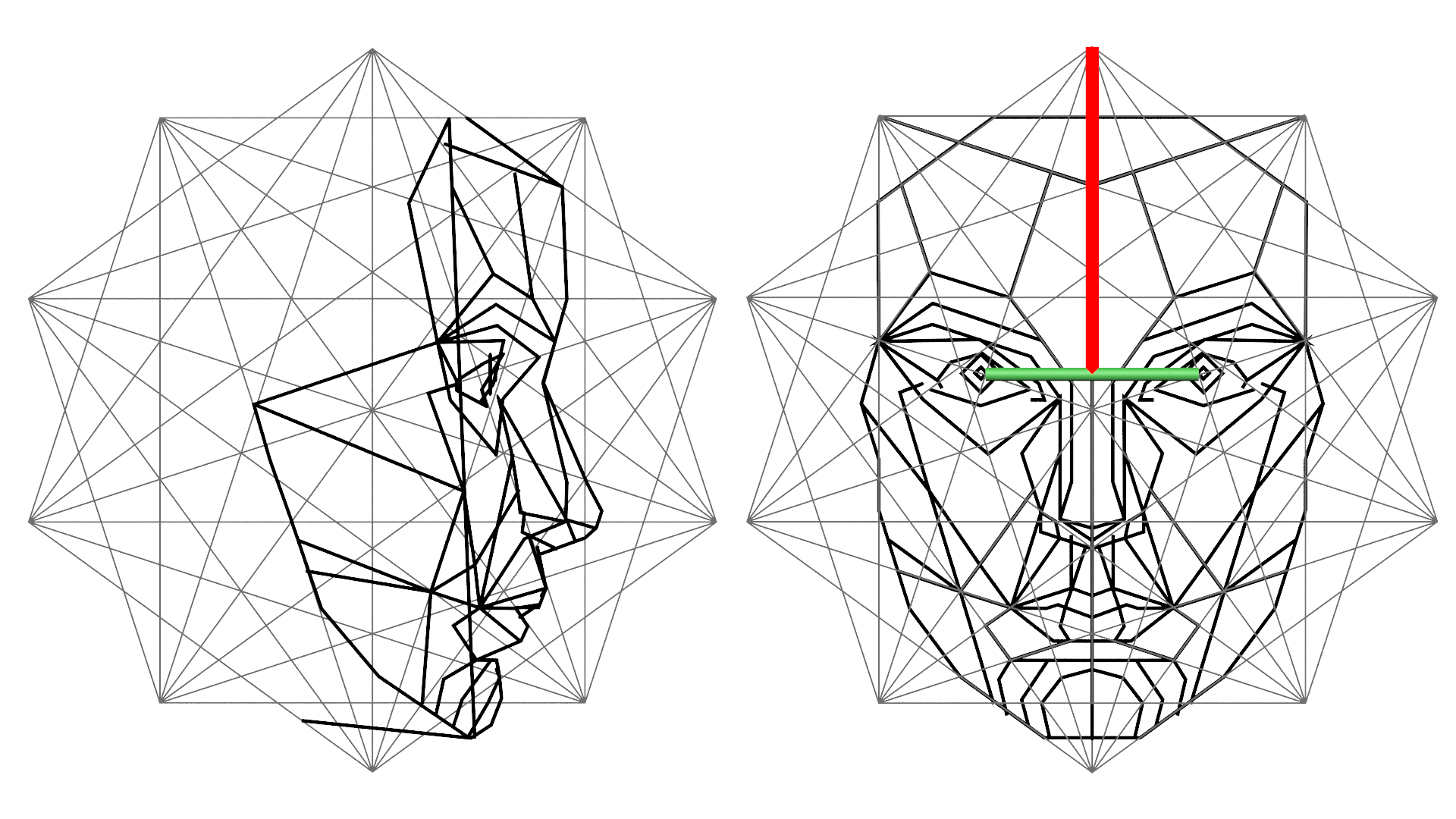
4. The Golden Mask in 3D
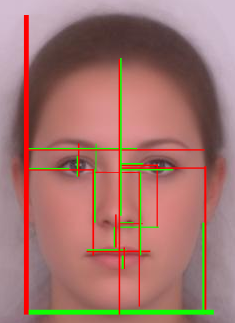
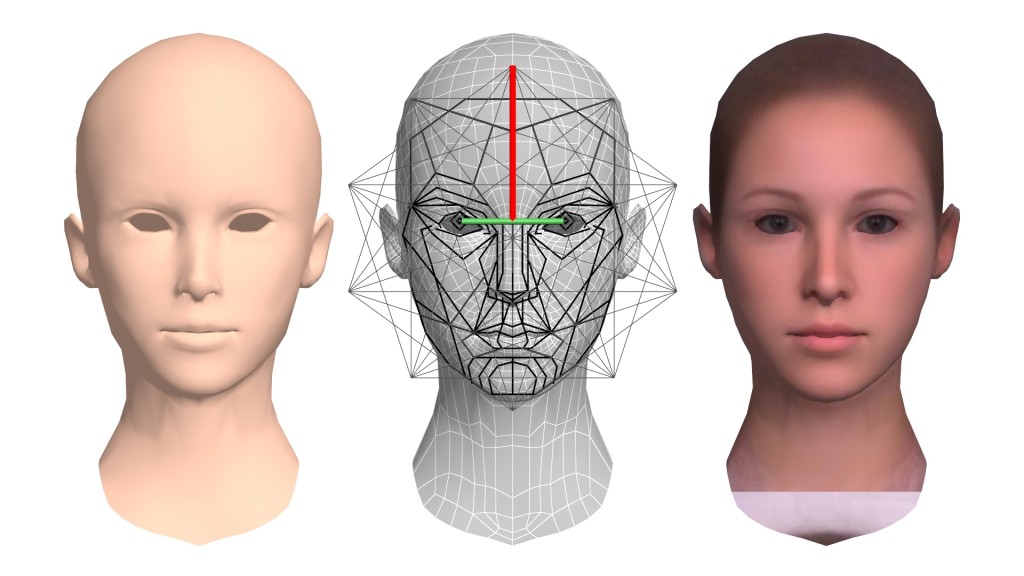
Dr. Stephen R. Marquardt has the idea to create a beauty mask for plastic surgery and applies on average human face the pattern of two pentagons. The starting points to determine the correct positioning of the facial features are the left and the right pupillary. By multiplying this distance with we get the height (red line) and place it onto the midpoint of the eye distance (green line). At top of this line is the first vertex of the first equilateral pentagon. By mirroring this in its middle we get the second (P2).
<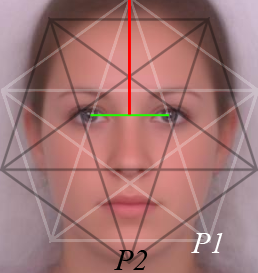


Figure 8: The phi mask applied to the average face (the female beauty mask downloaded from: http://www.beautyanalysis.com/index2_mba.htm).
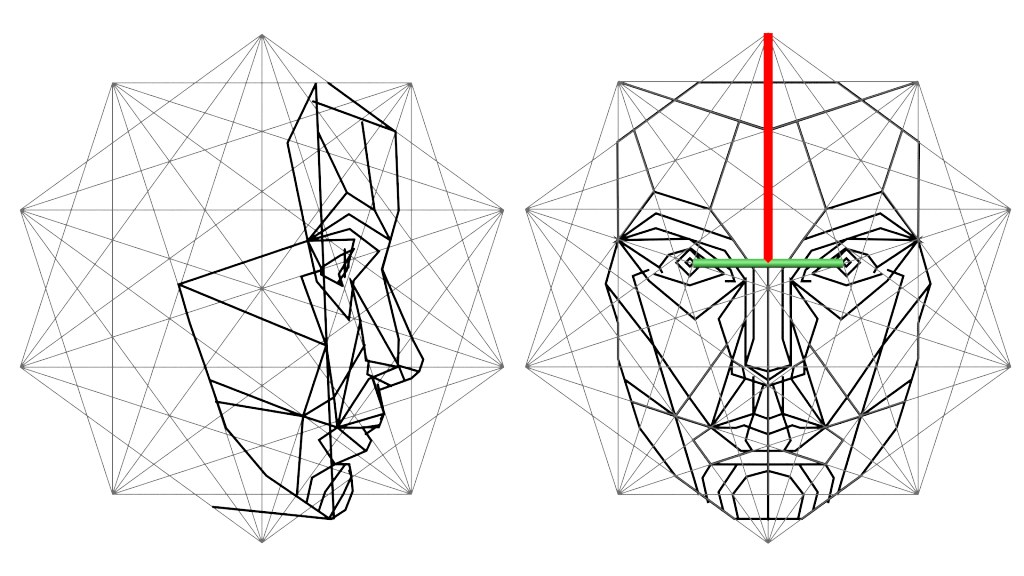
With the positions of the two shapes now we can make an overlay with the existing Phi Mask from Dr. Stephen R. Marquardt (Figure 8). Based on the graph we see that the proportions of the Golden Mask are ideal applicable to the average face. The attraction appears to be linked with the right proportions and the proportions of the result our analysis with the real human face. This technique is perfect to control shapes of a photo or a drawing. But how can we transfer the Golden Ratio or Phi mask on an unfinished 3D model and to improve our model to use? The solution is simple: We take the left and front view of the mask and reconstruct it in 3D. The template here is a pattern that provides scientific information also on the well-formed proportions in the depth of the face. So we can exactly model this splines in 3D space
Figure 9: Front and left view of an virtual 3D construction of the Phi Mask
We can adapt the face mesh e.g. with the vertices in a lowpoly mesh. Use the Soft Selection with more faces in your face or use MAXScripts when using 3ds max (5). You can download the PhiMask3D.max ( a 2010 .max – file) at my website (www.vali.de).
Figure 10: The 3D Phi Mask applied to a human face model (Face mesh by Solveigh Jäger (7))
Note: The 3D modeling process is not just a linear workflow with some predefined design rules or patterns which can just be applied. It is a dynamic development with many different influences. The digital human face in 3D is often designed by flavor and intuition. Constant critiques or design patterns are rarely used. The face mask should not be applied in a stadium where the mesh topology is unknown.
Figure 11: Left: The uncorrected imported mesh (7), Middle: Application of the 3D Phi Mask on the facial model during the correction process, Right: The new mesh and with the photo texture of the average female face image from the FaceResearch Lab.
Note: The 3D modeling process is not just a linear workflow with some predefined design rules or patterns which can just be applied. It is a dynamic development with many different influences. The digital human face in 3D is often designed by flavor and intuition. The face mask should not be applied in a stadium where the mesh topology is unknown.
5. The Golden Mask in 3D
It is not advisable to model a face that emanates from the Phi mask. The mask should always be applied to an existing mesh with new topology. The reason is clear: One is tempted to use the Phi face over and over. The problem of course is that the 3D artist is not forced to introduce new, perhaps better patterns of design and meshes with more or another character. By applying the mask we do not run into danger that all faces look alike. The 3D Phi Mask is a just a simple template to control the proportions of the Golden Ratio.
6. References
1. Wikipedia. Wikipedia. [Online] December 27, 2009. [Cited: April 20, 11.] http://en.wikipedia.org/wiki/Stephen_R._Marquardt.
2. Holland, Erik. Maquardt’s Phi mask. [Online] January 4, 2008. [Cited: June 20, 2011.] Background. http://www.femininebeauty.info/stephen-marquardt-phi-mask-refuted.
3. Pacioli, Luca. Woodcut from the ”Divina Proportione”. Venice : s.n., 1509.
4. Schnorch. Wikipedia. [Online] May 3, 2010. [Cited: June 20, 2011.] http://de.wikipedia.org/w/index.php?title=Datei:Human_head_proportions.svg&filetimestamp=20100503192018.
5. Rachel Mc Donnell, Ann McNamara. Application of the Golden Ratio to 3D Facial Models. [Online] 2003. [Cited: June 20, 2011.] http://mrhoyestokwebsite.com/AOKs/Maths/Related%20Articles/Golden%20Mask.pdf.
6. Topogun. Topogun Home. [Online] http://www.topogun.com/.
7. Jäger, Solveigh. Human face model. 2011.
8. Elisabetta Drudi, Tiziana Paci. Zeichnen für Modedesign. Mailand : The Pepin Press, 2001. 90 5496 094 9.